Scoring
QO is founded on a heuristic, the Occam method, which is based on Occam’s razor: the contention that, given a set of otherwise equivalent explanations, the explanation requiring the fewest apparently arbitrarily contrived elements is to be preferred. It is a method for deriving and evaluating an explanation tree. In QO, we apply the Occam method to determine in which sequence in which hypotheses about the universe should be examined.
Occam's razor is normally regarded as an aesthetic guideline, but in QO it is an imperative. If the universe came into existence out of absolute nothingness, then the simplest explanations for fundamental phenomena are the most credible.
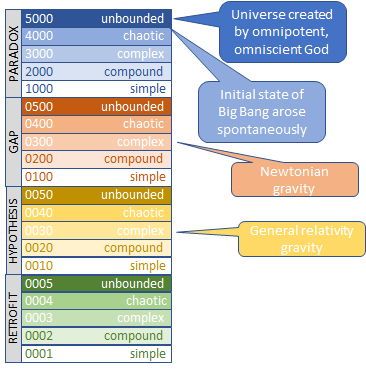
The basis for the Occam method is a scoring mechanism for each explanation on the basis of their profundity and complexity, to produce an Occam score. We use the following descending sequence of profundity classes:
-
Paradox: there is an apparent contradiction within or associated with the explanation. For example, we have no explanation for how the initial state of the Big Bang came to be, and the idea that something arose out of nothing is contrary to common sense, in other words a paradox.
-
Gap: the assumption that for some phenomena associated with the explanation there is a yet to be found viable sub-explanation. For example, we have no explanation for the existence of dark matter, which produces a gap in our explanations.
-
Hypothesis: the explanation is based on a concept, not itself observed as such, of which the existence makes the explanation workable and complete, as considered at the level of abstraction at which the abstraction is formulated. For example, the concept of phlogiston was a hypothesis to provide an explanation for combustion. Note that the concept on which a hypothesis is based will itself require explanation, and that this explanation may involve a gap or even a paradox.
-
Retrofit: a constant, the value of which is not derived from first principles, but is chosen to make the explanation fit the observations.
The complexity of an objection is determined by the number of explanatory elements that need to have particular values for the objection to be countered, on a scale 1 (simple), 2 (compound, i.e. several, more or less independent explanatory elements), 3 (complex, i.e. multiple explanatory elements which influence each other), 4 (chaotic, i.e. very many inter-related explanatory elements) to 5 (unbounded, i.e. it is not possible to set an a priori limit to the number of explanatory elements).
We regard one explanation as being better than another if it has a lower profundity class: paradoxes rank last, gaps second last, hypotheses second, and retrofits first. If two explanations have the same profundity, the explanation with the lowest complexity is to be preferred. This enables us to rank explanations according to their Occam score, which consists of a digit for each profundity category, starting with paradoxes. For example, 4102 means that there are 4 points for paradoxes, 1 for gaps, none for hypotheses, and 2 for retrofits.
The method
The Occam method involves the following steps to find the preferred explanation for a given set of phenomena:
-
Identify the phenomena for which you want an explanation. Be careful to not to leave out related phenomena just because you don't have an adequate explanation for them: that is framing, which is intellectually dishonest. Note that it is important to identify the phenomena as objectively as possible. Without agreement on the phenomena, the Occam Method cannot produce agreement on the credibility of explanations.
-
Itemize the explanations that either suggest themselves, or are given, or both. These are the level 1 branches of the explanation tree.
-
For each explanation, identify and score the explanatory elements, that is the sub-explanations that must be valid for the explanation to be complete. For example, an explanation which applies the concept of dark matter must have a sub-explanation which accounts for the existence of dark matter. Use that to score the explanation, including all the explanatory elements that are required for it to be viable, to derive a coordinate for each of the profundity classes. Where the explanation tree has an ‘or’-join (i.e. only one of the sub-explanations needs to be true for the explanation to hold), use the lowest score of the sub-explanations. Where it has an ‘and’-join (i.e. all of the sub-explanations need to be true for the explanation to hold), take the highest score per digit of these sub-explanations.
-
Strip the score of values which indicate a spurious accuracy, retaining only the scores due to explanations which are separated by at most two intermediate values in the ranking order, ignoring lower profundity classes. For example, 4050 becomes 4000, because there are many intermediate values between 4000 and 0050, whereas 1300 stays 1300, because only the values 0400 and 0500 come between 0300 and 1000. Insert the explanation into the explanation tree.
The lowest ranking explanation is the preferred explanation.
Credibility implications of scores
An explanation cannot be more credible than the least credible explanatory element which must be true in order for the explanation to fully account for the phenomena that are to be explained. In consequence, only absolute Occam scores are meaningful when discussing the credibility of an explanation.
This means that any explanation that assumes the Big Bang has an Occam score of at least that of the Big Bang itself – namely 5000 - regardless of how credible it would be if the Big Bang could be taken for granted. It also means that if two explanations both assume the Big Bang, there is no particular reason to prefer one over the other, even if they have markedly different Occam scores relative to the Big Bang. To give an analogous example: an explanation for the Hebrew slaves escaping from Egypt which maintains that an omnipotent, eternally existing God parted the Red Sea for them, is not essentially less credible than an explanation which depends on an omnipotent, eternally existing God, but denies this God’s miraculous intervention in this particular case.
Conversely, anything which would make the least credible explanatory element more credible would impact the credibility of all the explanations which depend on it. For this reason it makes sense to determine Occam Scores relative to the Big Bang, or whatever other explanatory element determines the absolute Occam Score.
However, this does not mean that relative Occam scores useful only in order to modify Occam scores efficiently. If it can be shown for some explanation that all other explanations, whether explicitly postulated, sensed or even so alien to us that we are incapable of conceiving them, must have higher Occam scores, then this explanation is credible, even if its absolute Occam score makes it incredible. However, such a situation is extremely unusual. The proposition that an initial quantum arose out of absolute nothingness falls into this category, because every other possible explanation must of necessity have a higher Occam score. That is why we are justified in comparing sub-explanations which follow on from QO on the basis of their relative Occam scores.
The larger the separation between the Occam score of an explanation and the Occam score of the proposition that the explanation is false, the greater its credibility. This is discussed in detail in the lemma Credibility and proof.
Use in directing research efforts
Note that the preferred explanation is preferred on the basis of the current set of phenomena and the current understanding of the explanations. Either of these may change, resulting in some other explanation becoming preferred. In fact, it is expected that they will change. The preferred explanation is naturally the explanation that attracts the most research. This will turn up new evidence, which may lead to the elimination of unnecessary complexity and profundity, and hence an even lower Occam score, or perhaps lead to the conclusion that there are additional objections and/or that the objections are more serious than originally thought, leading to a higher Occam score. Those who dare to risk a selection bias may revisit unpreferred explanations that appeal to them and look for simpler subexplanations at the points where there were more serious objections, perhaps resulting in these explanations becoming preferred.
The current set of phenomena may change for a number of reasons. New observations may turn up. Or the fact that a satisfactory preferred explanation has been found may lead the researcher to expand his horizons.
Limitations of the method
The Occam method is a method for sorting a tree of related explanations. It provides no guarantee that the best explanation will be identified, because it evaluates only the explanations in the tree. There may be simpler explanations, in the sense of requiring fewer assumptions, which are not in the tree. And the method may be applied incorrectly. The fact that an explanation is preferred should not be regarded as final conclusion. For example, QO might turn out to produce contradictions of such a nature that the big bang becomes the preferred explanation for further analysis. That wouldn’t make the big bang theory more credible than QO, at least not immediately. The big bang theory would need to be explored to the same level of detail as QO for such a conclusion to be reached. The explanations need to be of comparable depth.
The Occam method depends in part on the assumption that, whatever the best explanation tree for the universe is, that tree is finite. There is not an infinite regression of explanations, even if our experience leads us to think there is. The ancients, at least some of them, knew that matter was composed of atoms. Early last century we learned that atoms are composed of electrons, protons and neutrons. Late last century we learned that these particles are composed of quarks. So it is natural to assume that quarks, in their turn, are composed of still smaller things, and so on, forever. But in a universe which has existed for a finite amount of time, in which natural law has somehow developed, it is more reasonable to expect that there is a finite number of explanatory regressions. More reasonable, in any event, than to extrapolate from three regressions to infinity.
Biases
The Occam method is biased, and that's a good thing. It tends towards universal explanations, because any phenomenon observed to be universal would require additional explanatory elements in order to be declared non-universal. It is biased toward adoption of the same explanation for diverse phenomena, because any explanation that fails to exploit the opportunity for such an adoption is necessarily more complicated than one that makes use of the adoption. Failure to adopt the explanation for falling apples in order to account for planetary motions results in explanations that are inherently more complex, and hence have a higher Occam score.
